지난 번에 이어서 Binary Search Tree 의 Delete 과정을 자세하게 알아보겠다. 앞의 Search 와 Insert에 비해 복잡하기 때문에 험난한(?) 여정이 될 것이다.
Delete Algorithm
- Do search() first
- If Search() fails, Delete() also fails
- If Search() succeeds
- Case 1 : Node has no Child
- Case 2 : Node has one Child
- Case 3 : Node has two Children
Case 1
- Correctness trivial

child가 없는 노드를 지울 때 아무 문제 없는지 살펴보자. 만약 8번 노드 왼쪽에 subtree 가 있으면 지워져도 그 subtree는 child가 없기때문에 문제가 없다. 왼쪽은 무조건 노드의 작은값이 들어가기 때문에 tree의 구조가 깨질일이 없다.
Assume Dummy Root

코딩 하기 편리하게 Dummy Root를 넣어 두고 가정한다.(이런 식의 Skill은 코딩이 편하게 되는 자주 쓰이는 Skill 중 하나이다.)
Code for Delete Case 1
|
1
2
3
4
5
6
7
8
|
int Delete(Node *N, Node *P)
{
if(N->l === NULL && N->r == NULL) {
if(N == P->l) P-> l = NULL;
else P->r =NULL;
delete N;
}
};
|
Case 2
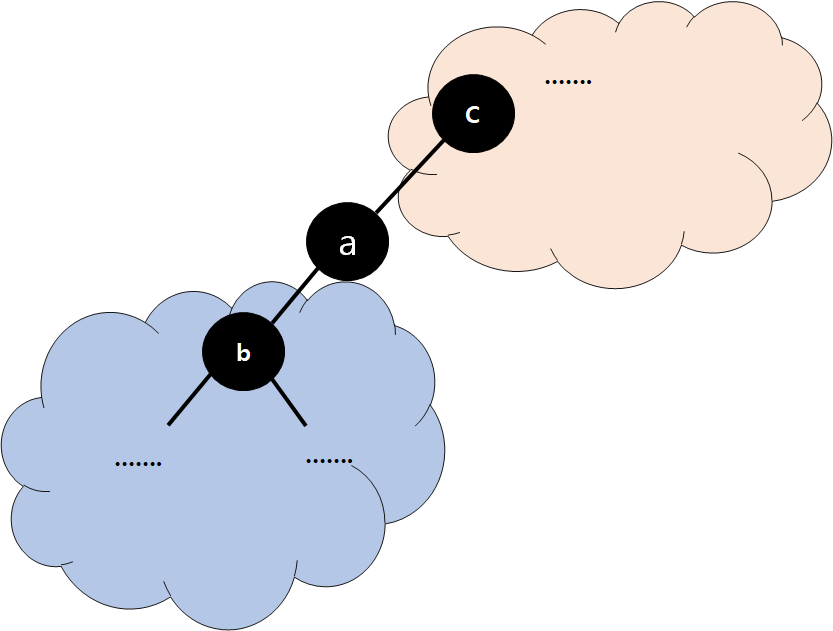
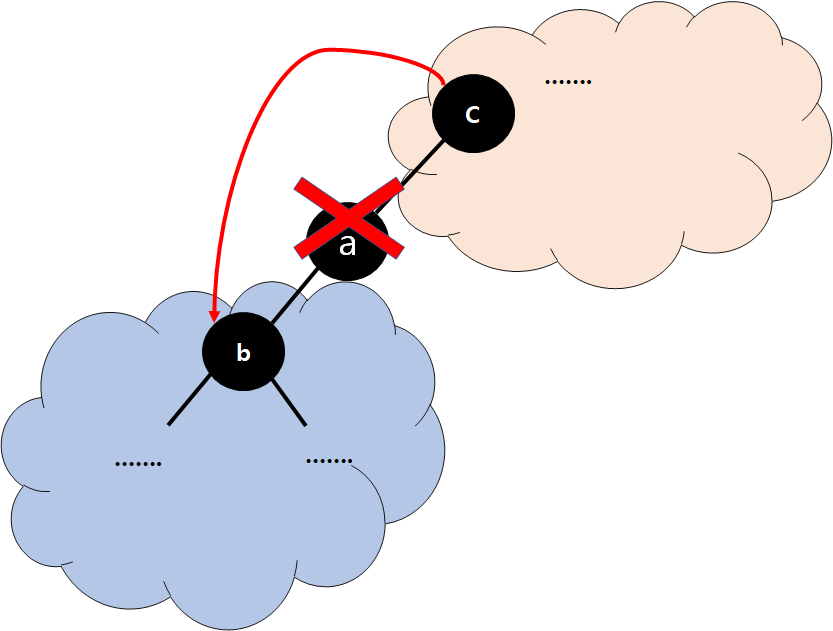
Case 2 Correctness
- Everything under b is not changed
- So, BST (Binary Search Tree) condition satisfied by all the Nodes in blue area.
- Every Key under b was already in the Left SubTree of c
- So, BST condition satisfied by all the Nodes in red area.
Code for Delete Case 2
|
1
2
3
4
5
6
7
8
9
10
11
12
|
int Delete(Node *N, Node *P)
{
else if (N->l != NULL && N->r ==NULL) // N의 왼쪽이 null이 아니고 오른쪽이 null인 경우
{
if(N == P ->l) P->l = N->l; //P의 Left를 하나 건너는 것
else P-> l = N->r;
}
else if (N->l == NULL && N->r !=NULL){
//Ditto
}
delete N;
};
|
Case 3
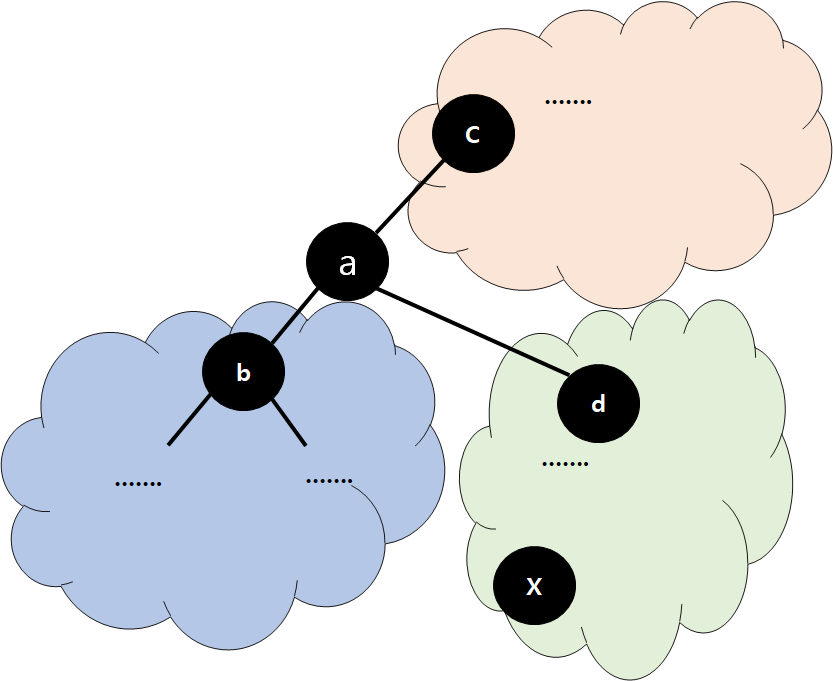
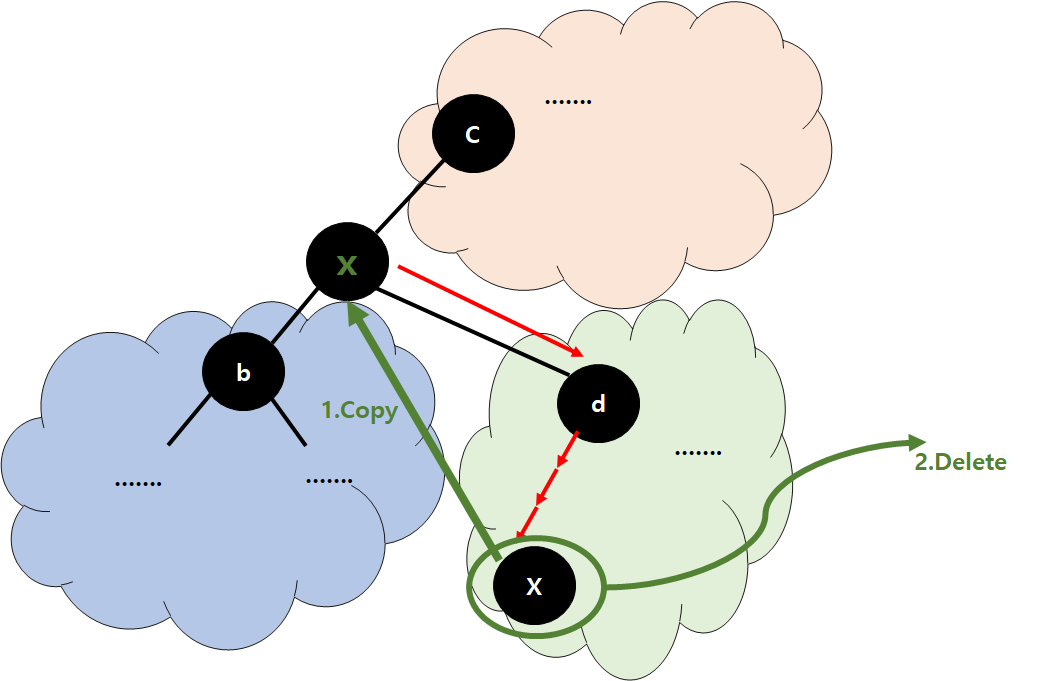
Case 3 Correctness
- If we sort all keys
- ...................a,x, ............... (-> tree 모든 node 한줄로 sorting)
- That is, x is right after a
- Why ???? let's accept that for now
- If we put x at the Node for a, then BST conditions are satisfied by all the nodes, except the original x (that's OK)
- Because no value between a and x is in the Tree
Code for Delete Case 3
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int Delete(Node *N, Node *p)
{
else if (N->l != NULL && N->r !=NULL){
Node *NN, *PP;
NN = N->r;
PP = N;
while(N ->l != NULL) {
PP =NN:
NN = NN->l;
}
N-> k = NN ->k;
Delete(NN,PP);
}
};
|
다른 방식의 증명을 알아보자.
Alternative Proofs
- Lemma : A BST is correct if and only if Search() succeeds for all values in the BST
- Proof
- By cases
- Case 1 : BST is correct -> Search() 성공
- Case 2 : BST is incorrect -> Search() 실패하는 것이 하나라도 있다.
Proof using the Lemma
- Case 1 : Trivial
- Case 2 : 설명필요.
- Case 3 : 설명필요.
- Why is this true? -> .........a, x, ........
- If you consider only under a, then it is obvious
- But, what about the red area?
- Any value between a and x there?
- Continuity Lemma
- All Key values in a SubTree appears continuously in the Sorted List
- Proof by top-to-bottom induction
-
Continuity Lemma Intuition

Proof
- Induction from Root to Leaf
- Base: For Root, the property is obvious (It's the whole sequence)
- Step: Assume the property holds for a node X. Let's think about its two children L and R

Search Performance
- Given a fixed Tree
- Worst Case: O (Height)
- Average Case : There are not many nodes near the top!
- Considering All Possible Trees
- Worst Case: O(n)
- Average Case: Consider only insert, values 1,2, ... , n are inserted in random order
- Random order: all of n! permutations are equally likely
- Probability that the root has 1 is 1/n, 2 is 1/n, ... , n is 1/n
- E(Height of n Nodes):
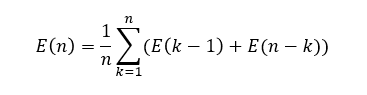
- Turns out to be O(log n), also with high probability(대다수의 경우 높은 확률로)
다른 성능 평가와 다르게 조금 애매모호(?)한 감이 있지만, 우리는 느려질 확률이 매우 낮다는것을 짐작을 할 수가 있다.
'프로그래머, 보안 관련 지식 > 자료구조' 카테고리의 다른 글
| 자료구조 : Tree(3) - AVL Tree - (0) | 2020.05.15 |
|---|---|
| 자료구조: Tree(1) - Binary Search Tree - (0) | 2020.05.04 |
| 자료구조: Linked List (0) | 2020.04.28 |
| 자료구조: Equivalence Relation(동치 관계) (1) | 2020.04.26 |
| 자료구조: Stack & Queue (3) (0) | 2020.04.25 |



