이번 포스트에서는 동치관계에 대해 알아보는 시간을 가지겠다. 지난번에 이이서 stack 과 queue를 활용한 방법들을 보여줄 예정이다.
Contents ( 이번 포스트의 내용 )
-
Another Application of stack and DFS
- What is an Equivalence Relation?
- What is an Induced Equivalence Class?
- How to find the Induced Equivalence Class given an Equivalence Relation?
- Performance Considerations
Definition of Equivalence Relation
- First, Definition of Relation
- Given a set A, a Relation on A is any subset of AxA
- Ex) A = {1, 2, 3, 4}, R = {(1,3), (3,4), (1,1), (2,2)}
- We write 1R3 to mean (1,3) ∈ R
- An extreme example
- Relation '<' on N (Natural Numbers)
- '<' = {(1,2), (1,3), ..., (2,3), (2,4), ... }
- 2<4 means the same thing as (2,4) ∈ <
- Equivalence Realtion is when a Relation is ...
- Reflexible : For all possible a , aRa
- Symmetric: For all possible a and b , aRb implies bRa
- Transitive: For all possible a,b and c, aRb and bRc implies aRc
- Intuitively, Equivalence Relation can be thought of as some relation which means some properties are the same
- People with same height, hair color, etc.
Induced Partiton
- Given an Equivalence Relation, a Partition is naturally induced
- Definition : Maximal subsets 𝐴_(𝑖 ) where if and only if a ∈ 𝐴_(𝑖 ) and b ∈ 𝐴_(𝑖 ) then aRb
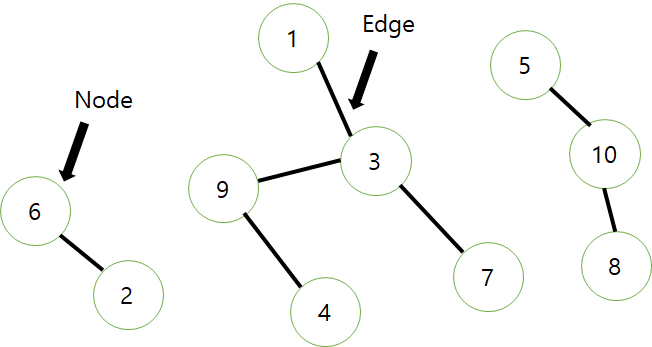
위의 그림을 보자. 눈으로 보면 우리는 세 개의 그룹으로 묶여있다는 것을 한눈에 알 수 있다. 그러나 컴퓨터는 이들을 어떻게 구분할까 컴퓨터에서 그룹을 구분하는 것을 이번 포스팅에서 알아 볼 것이다.
How to find the Induced Partition?
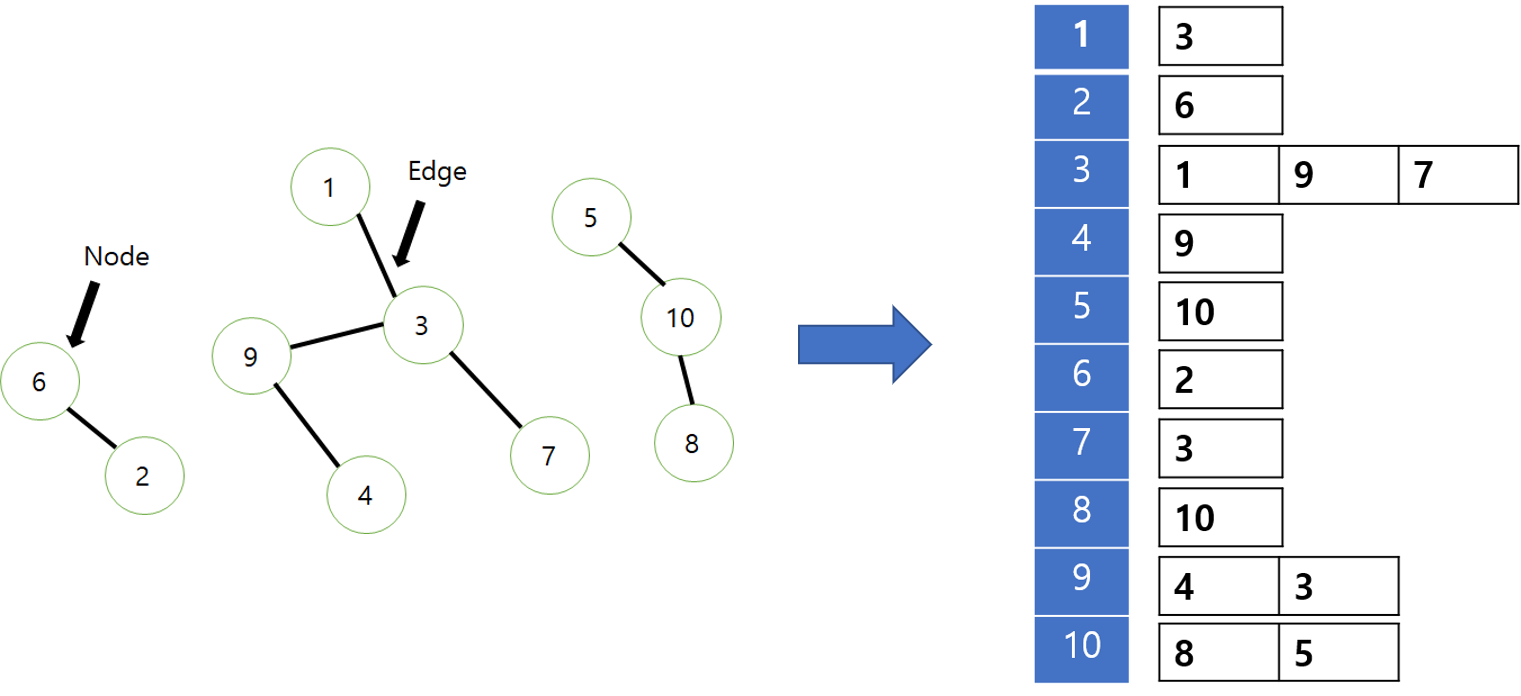
위의 그림을 컴퓨터가 알아 볼수 있게 표현하려면 다음과 같은 작업을 한다.
1 3
3 9
6 2
5 10
7 3
4 9
8 10
이런식으로 쌍들이 기본 입력이 된다. (배열 등의 방식으로) 그러나 이런 방식은 연결된 것들을 찾을 때 일일히 처음부터 끝까지 찾아봐야한다.(결과적으로 느려지게 된다.) 그래서 위의 것을 좀더 가공을 해서 저장을 한 다음에 쓴다. 총 2가지 가공 방법을 알아볼 것이다.
** One Assumption
- Input is given in Minimal Form ( 줄일 수 있는 한 최대한 줄임, 필요한 것은 빼지 않음 )
- No deducible pairs are given
Minimal form이 무엇이냐 하면 유추 가능한 관계들을 모두 최소한으로 생략했다는 것이다. 그림을 참고하면서 설명하겠다.
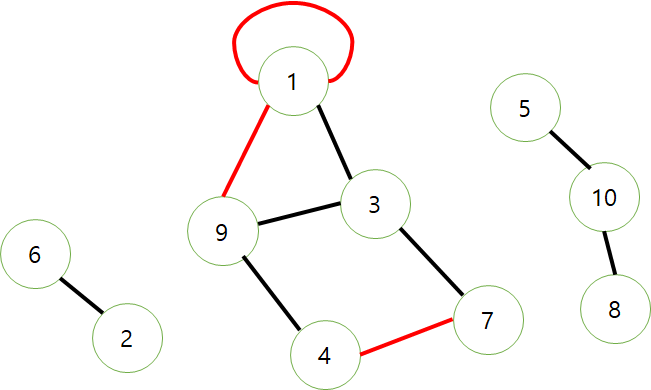
앞의 3그룹에서 우리는 1에서 1을 가리키는것 1에서 9를 가리키는 것 이러한 관계들이 있을 것이라고 유추 할수 있다. (빨간색 edge) 그러나 이러한 빨간색 edge들이 없어도 우리는 3그룹을 구분하는데 전혀 지장이 없다. 이런것들이 생략되었다는 뜻이다.
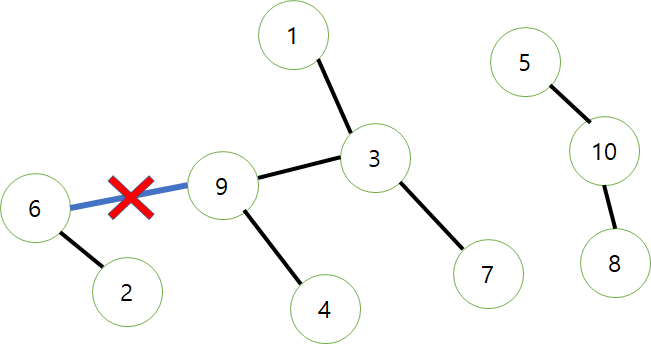
만약 6과 9 사이에 edge가 있으면 기존 3개의 그룹에 영향이 간다. 이러한 영향력 있는 edge들은 생략하지 않았다는 이야기다.(결과적으로 앞의 그림은 6,9과 연결되있는데 생략되었을리는 없다는 이야기이다.)
노드가 n개일때 그럼 최대 몇개의 edge가 주어질까 ? n-1개의 edge가 최대 일 것이다. n-1이 넘어가게 되면 싸이클(순환하는 형식)이 생기게 되어 버린다.
자 이제 첫번째 form을 살펴보자. 이 방식은 일단 메모리를 좀 많이 쓰게 되고, 아마도 느릴것이다.
Let's use DFS
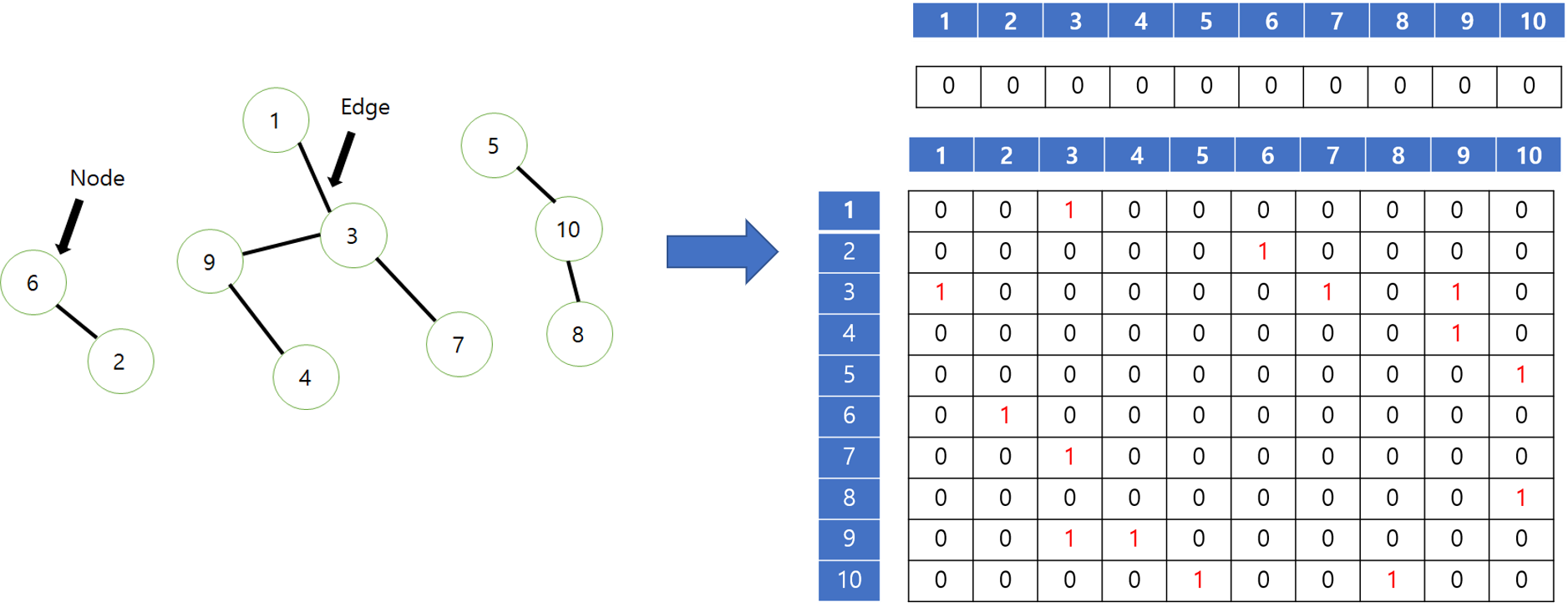
다음과 같이 그림을 2차원 배열 형식으로 나타내보자. 배열의 가로 세로는 노드의 번호를 나타내고 10X10 표에서 1 이라고 체크 되어 있다는 것은 노드 2개가 서로 연결이 되어 있어서 바로 갈 수 있다는 뜻이다. 그리고 나서 한번 출발을 해 갈 수 있는 곳은 전부 다 가보고 끝나게 될것이다. 이는 지난번 다룬 미로찾기 방법과 유사하다. (DFS의 특징) 맨 위에 따로 뽑아놓은 한줄은 마킹을 하기 위한 곳이다. 출발은 아무곳에서나 하면 된다. 여기서는 1부터 시작했다고 가정해보자.
1번에서 시작하면 우선 1번에 *라고 마킹을 하고 시작할 것이다. 그리고 나서 1번 에서 인접하는 곳을 찾아 볼것이다. 1이 나올때까지 찾는것이다. 세로로 먼저 찾아본다고 했을 때 맨 처음으로 3에 1이 체크된 것을 보게 될 것이다. 그러면 마킹지의 3번을 보고 0이라고 되어있으니 한칸 전진하게 될 것이다. (이를 나타내는 위치값이 당연히 필요하게 될 것이다.) 바로 3번에 *이라고 마킹을 한다. 그리고 나서 3번에서 다시 시작하게 된다. 3번 자리로 가서 다시 세로부터 쭉 보기 시작한다. 그러면 맨 처음 1이 마킹이 된것을 발견 할 수 있다. 그럼 마킹지로 가서 1을 확인해 본다 아까 우리가 1부터 시작해서 1에 마킹이 되어있는 것을 보게 될 것이다. 그러면 전진을 하지 않는 것이다. ( 넘어 간다는 뜻이다.) 이런식으로 한번 DFS를 돌리면 다음과 같다. 그런데 한가지 성능 적인 문제에서 이슈가 있다. 7번에서 넘어 갈때 8번 부터 볼것이냐 아니면 다시 1번부터 차근차근 볼 것이냐에 따라 성능의 차이가 날수 있다.
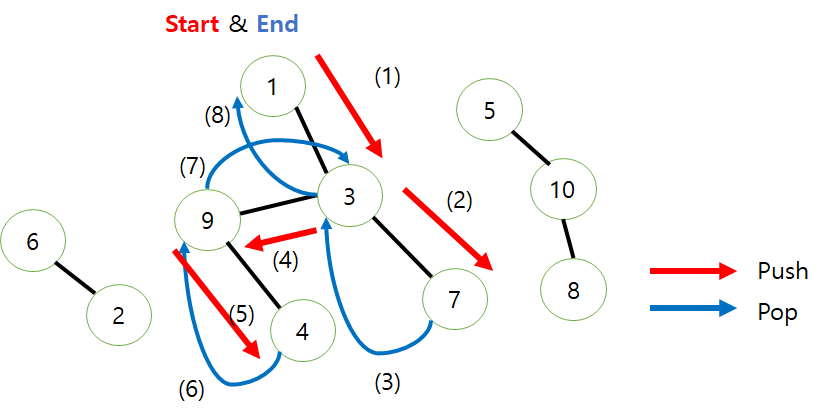
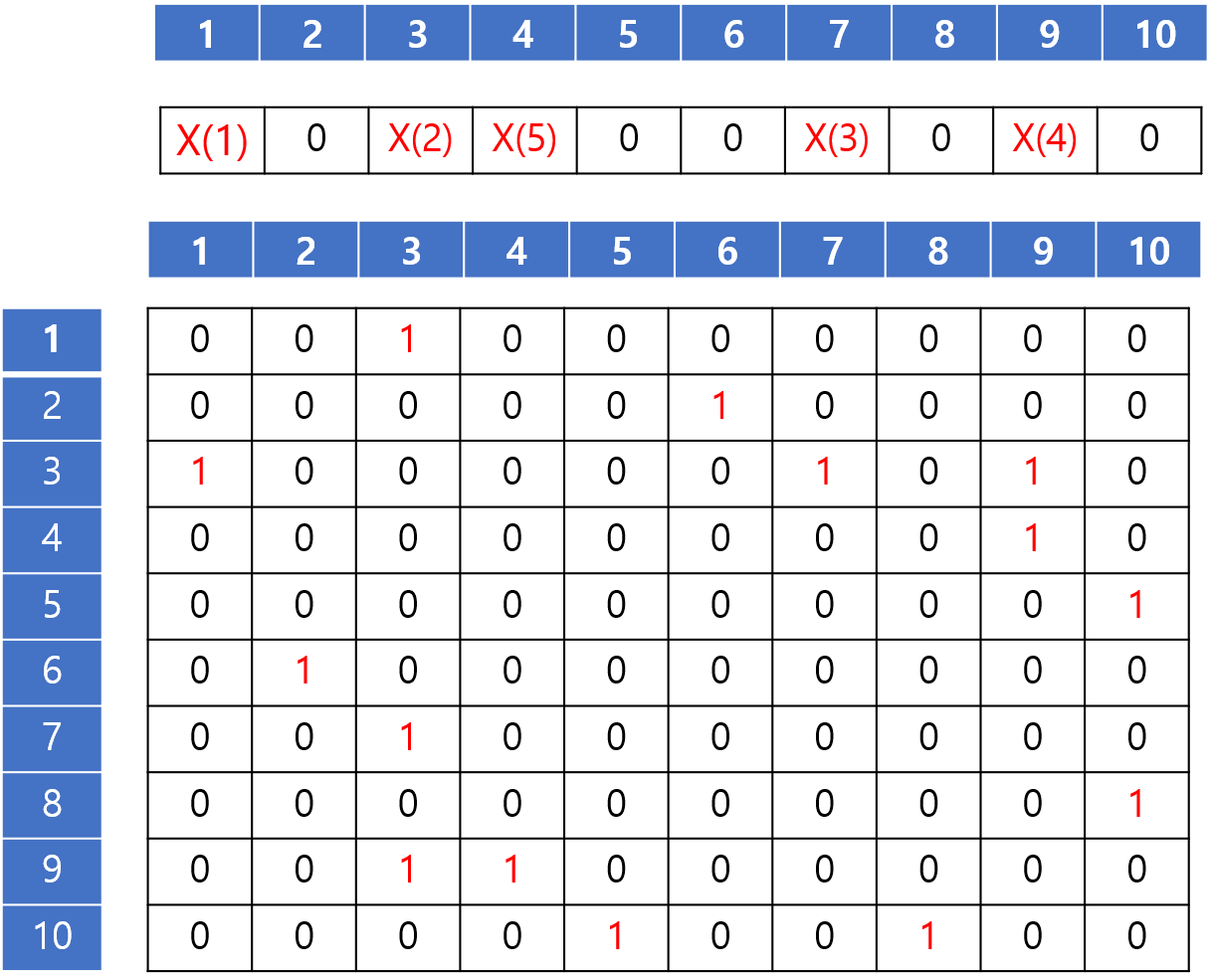
자, 이제 한번 돌았으니, 다시 돌아봐야하는데 3번 7번 9번 4번에서는 시작할 필요가 없다는 것을 알 수 있다. 그들을 제외하고 안가본 곳에서 시작하게 한다. 마킹지의 0이 있는 곳중 아무데나 하나 부터 시작하여 아까와 같은 방법으로 찾아 나가면 된다. 그런데 여기서도 성능적인 문제의 이슈가 될 수 있는게 2,6에서 끝나고 0을 찾을 때 3번부터 찾을 거냐 아니면 다시 처음 부터 스캔 할 것이냐에 따라 성능에 차이가 생길 수 있다. 이것에 따른 성능이 얼마나 차이나게 되는지 알아보자.
Performance Analysis
- Categorize time used
- On the Marker
- Two options : Start from beginning every time or remember last location
- Marking : O(n)
- Beginning: O(n^2)
- Remenber: O(n)
- On the Stack
- O(n)
- On the Matrix
- Two Options : Start from beginning every time or remember last location
- At each Row : O(n^2) and O(n)
- On the whole: O(n^2) either way
- On the Marker
전체적으로 결국 O(n^2) 이 되어버린다. 이를 줄이려면 어떻게 해야할까? 다음과 같은 방법으로 시간을 줄일 수 있다.
Equivalence Relation Example
이런식으로 아까의 매트릭스의 크기를 줄일 수 있게 된다. 한번 돌면서 메모리를 잡고, 두번 돌면서 값을 집어넣는 식으로 하면 이와 같이 만들 수 있을 것이다. 이런식으로 줄일 수 있을수 있었던 이유는 1의 개수가 작기 때문이다. (1의 개수가 많으면 아까 방법을 쓰면 된다.) 그러면 얼마나 성능이 향상이 되었을 지 알아보자
Performance Analysis
- Categorize time used
- On the Marker
- Two options : Start from beginning every time or remember last location
- Marking : O(n)
- Beginning: O(n^2)
- Remenber: O(n)
- On the Stack
- O(n)
- On the Matrix
- Two Options : Start from beginning every time or remember last location
- At each Row : O(n^2) and O(n)
- On the whole: O(n^2) and O(n)
- On the Marker
아까와 다르게 전체 시간복잡도는 O(n)이 된다.
이러한 동치 관계를 응용해서 예를 들어 페이스북 친구가 같은 그룹에 속하는지 등에 대해 알 수 있다.
다음 포스팅에서는 새로운 자료구조인 LinkedList 에 대해 알아보겠다.
'프로그래머, 보안 관련 지식 > 자료구조' 카테고리의 다른 글
| 자료구조: Tree(1) - Binary Search Tree - (0) | 2020.05.04 |
|---|---|
| 자료구조: Linked List (0) | 2020.04.28 |
| 자료구조: Stack & Queue (3) (0) | 2020.04.25 |
| 자료구조 : Stack & Queue(2) (0) | 2020.04.25 |
| 자료구조 : Stack & Queue(1) (0) | 2020.04.17 |


