이번 포스트에는 자료구조에서 자주 쓰이는 배열에서의 Search, Insert, Delete 에 대해 알아보겠다.
Search, Insert, Delete
- 자료구조의 가장 중요한 연산들
- 책상 위를 보시오! (우리가 평소에도 많이 하는 작업들 공책에 쓰고 지우고...)
- 그렇다고 모든 자료 구조에 해당하는 것은 아니다.
- 예) 그래프
- Item: 저장되는 대상을 부를 이름
- 정수만 가능한 것으로 생각을 하자.
임의의 배열을 통해서 알아보자.
Array

임의의 배열의 형태를 생각해보자 배열은 index와 value로 구성되어있다.
그렇다면 위 배열을 토대로 배열 안에서 삽입, 삭제, 검색이 어떻게 이루어지는지 알아보자
How to Store Items in an Array?
- Packed vs Unpacked (빈자리가 있냐? 없냐?)
- 배열이 항상 가득 차 있는 것은 아니다.
- 빈 자리를 한 쪽으로 모은다?
- Sorted vs Unsorted
- item들이 정렬된 상태를 유지하느냐 아니냐?
총 4가지 경우에 대해서 성능이 어떤지를 알아보는 시간을 가져보겠다.
Case 1 ) Packed, Unsorted

- 가장 간단한 방법
- Item의 개수를 표시하는 변수가 따로 필요 하다.
- => 위 배열을 보면 item이 5개 있으니 어딘가에 5라고 저장 해놓으면 해결된다.
- Search : n개의 배열에서 어떤 값 x가 있는지 없는지 확인, O(n)
- Insert : [Search, O(n)], O(1)(상수시간)
- Delete : [Search, O(n)], O(1)
- *** Insert와 Delete는 보통 Search를 먼저 수행함
이 경우에는 별로 좋지는 않다. Search가 수행되어야 하는데 Search가 느린편이기 때문이다.
Case 2 ) Packed, Sorted
- Binary Search!
- Item의 개수를 표시하는 변수가 따로 필요 하다.

- Search : O(log n) (Binary Search 이용)
- Insert : 옆으로 하나씩 복사한다음 덮여씌우는 방식을 사용, [Search,O(log n)], O(n)
- Delete : [Search, O(n)], O(n)
- *** Insert와 Delete는 보통 Search를 먼저 수행함
아까보다 Search는 좋지만 Insert와 Delete에서는 그렇게 좋지 않음을 알 수 있다. 다만 Search만 주로 이용하는 곳에서는 유용하게 쓰일 수 있을 것이다. (ex) 전자사전 같은 검색위주의 서비스
Case 3 ) UnPacked, UnSorted
- 빈 자리들이 흩어져 있음
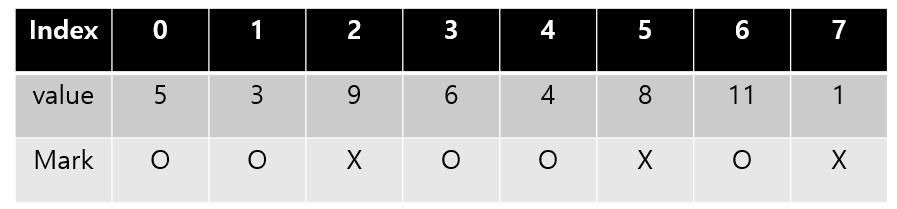
- Item 별로 사용중인지 아닌지 표시가 필요하다.
- Mark는 따로 배열을 만들던가 클래스 구조체를 이용해서 표현하는 식으로 생각하면 된다.
- Search : O(n) (단 ,앞서 봤던 packed, Unsorted 보다는 조금 안좋을수도 있다. unpacked 이기 때문에 한쪽으로 모으는작업 필요)
- Insert : [Search: O(n)], O(n) (빈자리를 찾아야 하기 때문에 )
- Delete : [Search: O(n)], O(1)( 안 쓴다고 마킹만 하면 되기 때문에)
그런데 이 경우에는 Insert에서 어떠한 기술 하나를 활용할수 있다.
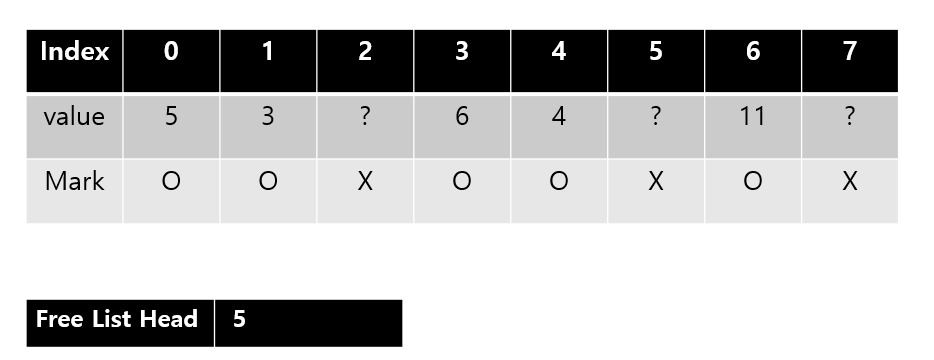
Free List Head 라는 변수를 하나 만든다. 5라는 뜻은 index 5번이 빈자리라는 뜻이다. 그러면 Free List Head에 모든 빈자리를 적으면 해결이 될까? 그렇지는 않다 빈자리는 시시각각 변하기 때문에 또 Free List Head에서 Insert Delete Search 작업을 해야하기 때문이다. 대신에 이렇게 활용한다. 다음 그림을 보자
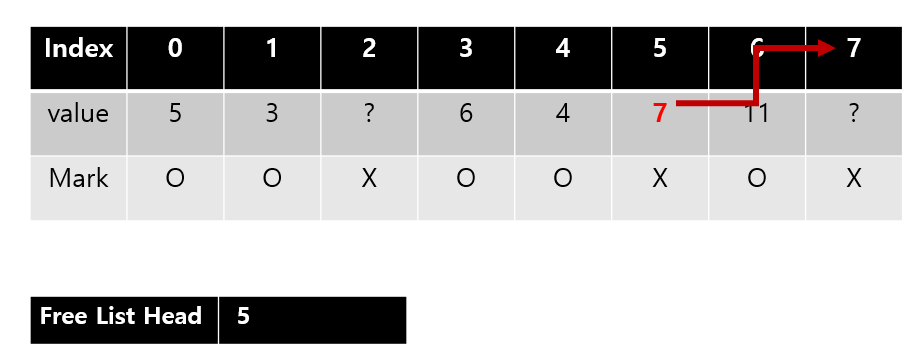
우리는 5의 값이 비어있다는 것을 알고 있다. 그러면 그곳에다가 7을 적는다. 7은 index 7을 뜻하며 그곳이 비어 있다고 약속을 하자.
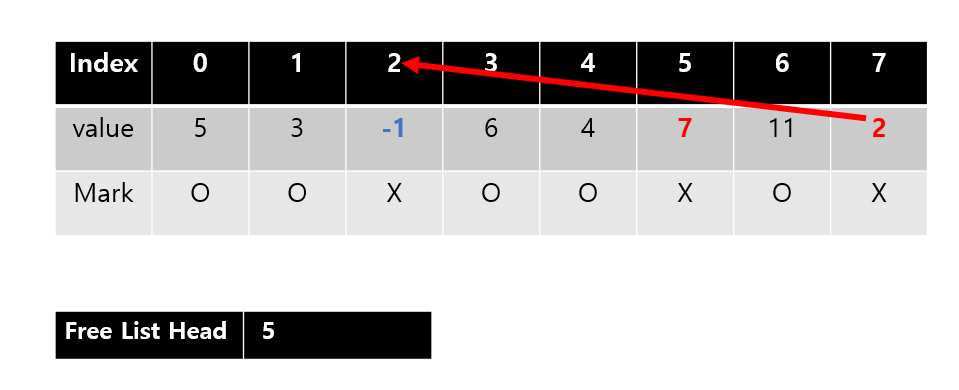
위와 비슷하게 7에는 2를 적어둔다. 역시 index 2를 가리키며, 그곳이 비어있다고 약속한다.
그러면 2에는 무슨 값을 넣어야하나? -1을 넣는다. -1은 index가 될수 없는 값이며 이는 끝났다는 것을 의미한다.
자 이제 Insert를 생각해보자. 어떤값 20을 넣는다고 할때 우리는 5번이 비어있음을 알수 있다. 5번에다가 20을 넣으면 된다. 그런데 20을 넣으면 이제 더이상 빈자리가 아니게 되어서 마크 값도 O로 변경 되어 있을 것이다.
그리고 Free List Head에 값도 변경해줄 필요가 있다. 5의 다음을 가리키는 7로 변경하면 insert가 성공적으로 수행된다.
성공한 배열은 다음과 같은 것이다.
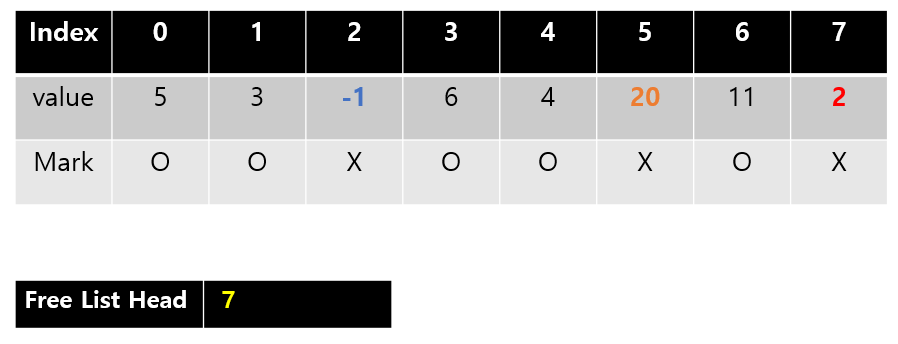
그러면 결과적으로 Insert: [seacrh O(n)] + O(n) (기술추가) -> [seacrh O(n)] + O(1) 로 바뀌게 된다.
이 기술은 Linked List 라고 불리는 기술로 다른 자료구조이다. 추후에 좀더 자세히 다룰것이다.
d이 기술의 대표적인 사용법은 우리가 알고 있는 파일 시스템, Free Block List on File System 에서 사용하고 있다.
Case 4 ) UnPacked, Sorted
- Binary Search!!! ... ... ??????????????
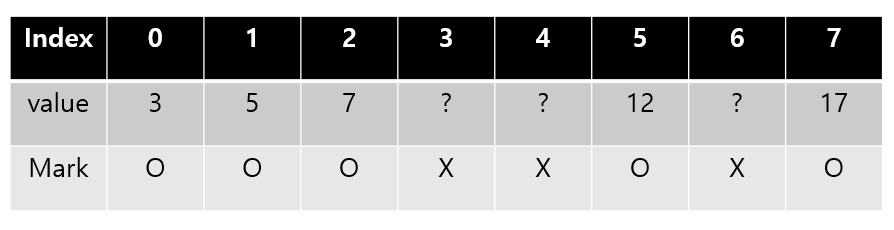
마지막 경우를 살펴보자 이 경우 우리는 Binary Search를 사용할 수 있는가? 빈자리가 있는데 중간을 잘라서 Binary Search를 사용할 수 있나? 이 경우에 하나의 기술을 이용한다. ? 표시는 우리가 이해를 편하기 위해 놓은 거지만 실제로는 어떠한 값이 들어가 있을것이다. 그렇다면 Mark을 무시하고 전체를 Sorting 하는 것이다. 지워진 값들까지 sorting이 되어 있도록 하면 Binary Search를 할수 있다. 예를들어 11을 찾는데 값을 찾았더니 marking 이 X 상태이면 그 값은 없는 값이라고 나타내면 된다.
- Search : O(n) -> 기술 추가 -> O(log n)
- Insert : [Search, O(log n)], O(n)(최악의 경우, 대부분은 이것보다는 2~3배 정도 나을 것)
- Delete : [Search O(log n)] , O(1)
이것으로 배열에 Insert Search Delete에 대해 알아 보았다. 이러한 자료구조는 많이 쓰이지만 성능이 중요한 곳에서는 조금 힘들것이다. 다음시간에는 좀 더 어려운 자료구조에 대해 배워보겠다.
'프로그래머, 보안 관련 지식 > 자료구조' 카테고리의 다른 글
| 자료구조: String Matching(2) (0) | 2020.04.17 |
|---|---|
| 자료구조 : String Matching(1) (0) | 2020.04.16 |
| 자료 구조 : Selection Sort, Merge Sort(2) (0) | 2020.04.15 |
| 자료 구조 : Selection Sort , Merge Sort (1) (0) | 2020.04.15 |
| 자료구조 시작 전 알기 (5) Arrays, Algorithms, Complexity, and Recursion (0) | 2020.04.14 |


